Kaip Ištraukti Šaknį?

Anksčiau, kai dar nebuvo skaičiuotuvų, studentai ir profesoriai turėjo rankiniu būdu apskaičiuoti kvadratines šaknis. Sukurta keletas skirtingų metodų, padedančių įveikti šį bauginantį procesą, pateikia apytikslį galutinį skaičių, kiti – tikslų. Norėdami sužinoti, kaip rasti skaičiaus kvadratinę šaknį naudojant tik paprastus metodus, skaitykite toliau.

Šaknies ištraukimas ranka – Pirmas žingsnis:

• Padalinkite savo skaičių į skaičius, iš kurių traukiasi sveika šaknis ir kuriuos sudauginus, gautųsi jūsų skaičius.
• Norėdami rasti kvadratinę šaknį pirmiausia pabandykite sumažinti savo skaičių iki skaičių, iš kurių traukiasi sveika šaknis.

Pavyzdys: jei norite ranka rasti kvadratinę šaknį iš 400, skaičių padalinkite kvadratinius koeficientus. Kadangi 400 yra 100 kartotinis, žinome, kad jis dalijasi iš 25. Mes žinome, kad 25 įeina į 400 16 kartų. 16, atsitiktinai, taip pat yra skaičius, iš kurio traukiasi sveika šaknis. Taigi, kvadratiniai koeficientai 400 yra 25 ir 16, nes 25 × 16 = 400. Tai parašytume taip: √400 = √25 × 16.

Šaknies ištraukimas ranka – Antras žingsnis:

• Ištraukite savo sugalvotų skaičių kvadratines šaknis. 
• Kvadratinių šaknų sandauga teigia, kad bet kokiems nurodytiems skaičiams a ir b, galioja ši formulė: √a × b = √a × √b.
• Dėl šios savybės dabar galime ištraukti iš jūsų sugalvotų skaičių kvadratines šaknis ir jas padauginti, kad gautume atsakymą.

Pavyzdys: ištraukiame kvadratines šaknis iš 25 ir 16, užrašome šitaip √25 × √16. Galiausiai 5 × 4 = 20.

Šaknies ištraukimas ranka – Trečias žingsnis:

• Realiame gyvenime skaičiai, iš kurių turėsite ištraukti kvadratines šaknis, dažniausiai nebus gražūs skaičiai, iš kurių išsitrauks sveika šaknis, pvz., toks kaip 400. 
• Tokiais atvejais gali būti neįmanoma rasti tikslaus atsakymo, kuris būtų tik sveikasis skaičius. 
• Tokiu atveju galite rasti atsakymą į mažesnę kvadratinę šaknį ir liekaną.

Pavyzdys: ištraukime 147 kvadratinę šaknį. 147 nėra dviejų skaičių, iš kurių išsitraukia sveika šaknis, sandauga. Negalime gauti tikslios sveikojo skaičiaus vertės. Tačiau galime rasti vieną skaičių, iš kurio išsitraukia sveika šaknis – 49. Kitas skaičius bus 3. Atsakymą rašytume šitaip: √147 = √49×3. Tada √49 × √3 = 7 × √3.

Šaknies ištraukimas ranka – Ketvirtas žingsnis:

• Naudojant paprasčiausią kvadratinę šaknį, paprastai gana lengva gauti apytikslį atsakymą.
• Vienas iš būdų apskaičiuoti atsakymą yra rasti skaičius, iš kurių išsitraukia sveika šaknis, abiejose kvadratinės šaknies skaičiaus pusėse. 
• Jūs žinote, kad skaičiaus dešimtainė vertė jūsų kvadratinėje šaknyje yra kažkur tarp šių dviejų skaičių, todėl galėsite atspėti.

Pavyzdys: √35 gali būti tarp 5 – 6, nes skaičius 35 yra tarp skaičių 25 ir 36, iš kurių galima ištraukti sveiką šaknį. Skaičiaus 35 kvadratinė šaknis turi būti nuo 5 iki 6. Kadangi skaičius 35 yra tik vienu skaitmeniu mažesnis už skaičių 36, galime užtikrintai teigti, kad jo kvadratinė šaknis yra tikrai mažesnė nei 6. Patikrinus skaičiuotuvu gauname maždaug 5,92 atsakymą.

Šaknies ištraukimas ranka – Penktas žingsnis:

• Pirmiausia sumažinkite skaičių iki mažiausių skaičių. 
• Nebūtina rasti skaičius, iš kurių išsitraukia sveika šaknis.
• Parašykite savo skaičių pagal mažiausius bendrus veiksnius. 
• Tada tarp skaičių ieškokite sutampančių pirminių skaičių porų. 
• Radę du pagrindinius skaičius, kurie sutampa, pašalinkite abu šiuos skaičius iš kvadratinės šaknies.
• Vieną iš šių skaičių padėkite už kvadratinės šaknies.

Pavyzdys: šiuo metodu suraskime kvadratinę šaknį iš 45. Mes žinome, kad 45 = 9 × 5, ir žinome, kad 9 = 3 × 3. Taigi, mes galime parašyti savo kvadratinę šaknį taip: √3 × 3 × 5. Tiesiog nuimkite 3 ir padėkite vieną 3 už kvadratinės šaknies. Atsakymas užrašomas taip: 3 √5.

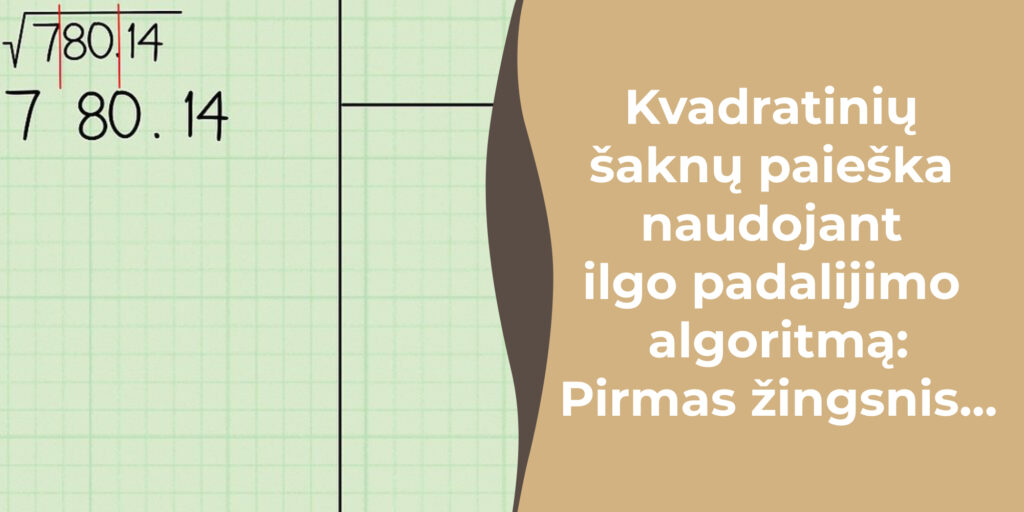
Kvadratinių šaknų paieška naudojant ilgo padalijimo algoritmą – Pirmas žingsnis:

• Šis metodas naudoja procesą, panašų į ilgą padalijimą.
  
• Pirmiausia nubrėžkite vertikalią liniją, perskiriančią lapą į dvi dalis.
• Tada nubrėžkite trumpesnę horizontalią liniją dešinės pusės viršuje, kad dešinė dalis būtų padalinta į mažą viršutinę ir didesnę apatinę. 
• Tada padalinkite savo skaičiaus skaitmenis į poras, pradedant nuo kablelio.
• Parašykite savo skaičių kairėjė pusėje viršuje.

Pavyzdys: pabandykime paskaičiuoti 780,14 kvadratinę šaknį. Kairėje pusėje viršuje parašykite „7 80. 14“. Nesvarbu, kad vienas skaitmuo neturi poros.

Kvadratinių šaknų paieška naudojant ilgo padalijimo algoritmą – Antras žingsnis:

• Pradėkite nuo kairiausios savo skaičiaus poros arba skaitmens, jei jis neturi poros.
  
• Raskite didžiausią sveikąjį skaičių n, kurio kvadratas yra mažesnis arba lygus kairiausiam skaičiui (arba porai).
• Tada ištraukite šio kvadrato kvadratinę šaknį.
• Šis skaičius yra n.
• Viršutiniame dešiniajame laukelyje parašykite n, o apatiniame dešiniajame laukelyje – n kvadratą.

Pavyzdys: kairiausia skaičiaus pora arba skaitmuo yra skaičius 7. Galima pasakyti, kad n = 2, nes tai yra didžiausias sveikasis skaičius, kurio kvadratas yra mažesnis arba lygus 7. Viršutiniame dešiniajame laukelyje parašykite 2. Tai yra pirmasis mūsų atsakymo skaitmuo. Apatiniame dešiniajame laukelyje parašykite 4 (2 kvadratą). Šis skaičius bus svarbus kitame žingsnyje.

Kvadratinių šaknų paieška naudojant ilgo padalijimo algoritmą – Trečias žingsnis:

• Iš kairės poros atimkite ką tik apskaičiuotą skaičių. 
• Parašykite šį skaičių po pirmąja dalimi ir atimkite, o po to parašykite savo atsakymą.

Pavyzdys: mes parašysime 4 žemiau 7, tada atimsime ir gausime tokį atsakymą: 3.

Kvadratinių šaknų paieška naudojant ilgo padalijimo algoritmą – Ketvirtas žingsnis:

• Šalia ką tik rastos atimtos vertės parašykite žemiau kitą skaičių porą, kurios kvadratinės šaknies ieškote. 
• Tada padauginkite skaičių viršutiniame dešiniajame laukelyje iš dviejų ir parašykite jį apatiniame dešiniajame laukelyje. 
• Šalia skaičiaus, kurį ką tik užsirašėte, palikite vietos daugybos užduočiai.
  

Pavyzdys: kita mūsų skaičiaus pora yra 80. Rašykite 80 šalia 3 kairiajame laukelyje. Tada padauginkite skaičių viršuje dešinėje iš dviejų. Šis skaičius yra 2, taigi 2 × 2 = 4. Apatiniame dešiniajame laukelyje įrašykite 4.

Kvadratinių šaknų paieška naudojant ilgo padalijimo algoritmą – Penktas žingsnis:

• Užpildykite tuščias vietas dešiniajame laukelyje tuo pačiu sveiku skaičiumi. 
• Šis sveikasis skaičius turi būti didžiausias sveikasis skaičius.
• Jį padauginus iš dešiniojo laukelio, rezultatas turi būti mažesnis arba lygus dabartiniam skaičiui kairėje.

Pavyzdys: užpildžius tuščias vietas skaičiumi 8, gauname 4 (8) × 8 = 48 × 8 = 384. Tai yra daugiau nei 380, todėl 8 yra per didelis, bet 7 tikriausiai tiks. Tuščiuose laukeliuose parašykite 7 ir išspręskite: 4 (7) × 7 = 329. Skaičius 7 tinka, nes 329 yra mažesnis nei 380. Viršutiniame dešiniajame laukelyje parašykite 7. Tai yra antrasis skaitmuo 780,14 kvadratinėje šaknyje.

Kvadratinių šaknų paieška naudojant ilgo padalijimo algoritmą – Šeštas žingsnis:

• Atimkite ką tik apskaičiuotą skaičių iš dabartinio skaičiaus kairėje. 
• Paimkite skaičių dešiniajame laukelyje ir atimkite jį iš skaičiaus kairėje, parašydami savo atsakymą žemiau.

Pavyzdys: iš 380 atimame 329 ir gauname 51.

Kvadratinių šaknų paieška naudojant ilgo padalijimo algoritmą – Septintas žingsnis:

• Dabar pakartokite 4 veiksmą ir parašykite likusią skaičiaus dalį. 
• Tada padauginkite skaičių viršuje dešinėje pusėje iš 2 ir parašykite jį šalia tuščio daugybos uždavinio („_ × _“).

Pavyzdys: Dabar mes susiduriame su dešimtainiu skaičiumi 780.14, kuris yra po kablelio. Dabartinio atsakymo viršuje dešinėje pusėje parašykite kablelį. Tada nuleiskite kitą skaičių porą (14) kairiajame laukelyje. 27 x 2 yra 54, todėl apatiniame dešiniajame laukelyje parašykite „54 _ × _ =“.

Kvadratinių šaknų paieška naudojant ilgo padalijimo algoritmą – Aštuntas žingsnis:

• Dabar pakartokite 5 ir 6 veiksmus ir užpildykite tuščias vietas dešiniajame laukelyje tinkamu tuo pačiu sveiku skaičiumi. 
• Šis sveikasis skaičius turi būti didžiausias sveikasis skaičius, kuris leidžia, kad rezultatas būtų mažesnis arba lygus.
• Atimkite ką tik apskaičiuotą skaičių iš dabartinio skaičiaus kairėje. 
• Paimkite daugybos uždavinio rezultatą dešiniajame laukelyje ir atimkite jį iš dabartinio skaičiaus kairėje, parašydami savo atsakymą žemiau.

Pavyzdys: 549 × 9 = 4941, kuris yra mažesnis už skaičių kairėje 5114. Skaičius 549 × 10 = 5490 yra per didelis, todėl 9 yra mūsų atsakymas. Viršutiniame dešiniajame laukelyje parašykite 9. Iš skaičiaus kairėje atimkite daugybos rezultatą: 5114 atėmus 4941 yra 173.

Kvadratinių šaknų paieška naudojant ilgo padalijimo algoritmą – Devintas žingsnis:

• Jei norite didesnio tikslumo, nuleiskite porą nulių kairėje ir pakartokite 4, 5 ir 6 veiksmus.
• Kartokite šį procesą ir suraskite savo atsakymo šimtąją, tūkstantąją ir t.t. dalis. 
• Tęskite šį ciklą, kol rasite atsakymą iki norimos dešimtainės tikslumo.